ME 2: Číslicová technika

Popis výrazů, se kterými pracuje obor číslicová technika.

Momentální třídění: Podle data vytvoření (vzestupně) Třídit chronologicky: Podle poslední aktualizace | Podle data vytvoření

Stránka: 1 2 3 (Další)
VŠE

Negace logického součtu

Tato funkce vznikne negací funkce OR. Označuje se NOR. Příslušný logický obvod vytvoříme sériovým zapojením OR a NOT obvodu.

$\mathbf{Y} = \overline{\mathbf{A}+\mathbf{B}}$

Značení

Pravdivostní tabulka

$X 1$	$X 2$	$Y$
0	0	1
0	1	0
1	0	0
1	1	0

Česky bychom řekli, že výstup Y je, pokud není přítomen signál na vstupu A nebo vstupu B nebo na obou vstupech současně.

Negace logického součinu - NOR

Klíčová slova:

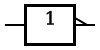
Logický součin

AND

Tento člen provádí funkci tzv. logického součinu (konjunkce).

$\mathbf{Y} = \mathbf{A}\cdot\mathbf{B}$

Značení

Pravdivostní tabulka

$X 1$	$X 2$	$Y$
0	0	0
0	1	0
1	0	0
1	1	1

Česky bychom řekli - vstup A a vstup B, nebo vstup A i vstup B musí být přítomen, aby byl také výstup.

Klíčová slova:

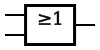
Logický součet

AND

Tento člen provádí funkci tzv. logického součinu (konjunkce).

$\mathbf{Y} = \mathbf{A}+\mathbf{B}$

Značení

Pravdivostní tabulka

$X 1$	$X 2$	$Y$
0	0	0
0	1	1
1	0	1
1	1	1

Česky bychom řekli, že pokud má hodnotu vstup A nebo vstup B, je výstup aktivní.

Logický součet

Klíčová slova:

Logická negace

Logická negace je funkce, při níž se obrací hodnota vstupního signálu na opačnou hodnotu. Matematicky vyjádřeno:

$\mathbf{Y} = \overline{\mathbf{A}}$

[čteme A non].

Značení

Pravdivostní tabulka

$X$	$Y$
0	1
1	0

Česky řečeno - výstup je když není vstup a obráceně. Ještě jinak,
logická negace převrací hodnotu vstupního signálu.

Klíčová slova:

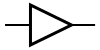
Zpožďovací člen - Buffer

Nejjednodušším logickým členem je buffer neboli zpožďovací člen, který realizuje funkci identity.

$\mathbf{Y} = \mathbf{A}$

Značení

Pravdivostní tabulka

$X$	$Y$
0	0
1	1

Negace logického součinu

Tento člen provádí funkci tzv. negovaného logického součinu. Je to nejběžněji používané hradlo. Propojením vstupů je schopno pracovat jako invertor. Lze pomocí něho realizovat většinu klopných obvodů.

$\mathbf{Y} = \overline{\mathbf{A}\cdot\mathbf{B}}$

Značení

Pravdivostní tabulka

$X 1$	$X 2$	$Y$
0	0	1
0	1	1
1	0	1
1	1	0

Česky bychom řekli, že výstup Y je, pokud není přítomen signál na obou vstupech A a B současně.

Klíčová slova:

Pravidlo asociativní

Platí, že:

A(B . C) = (A . B)C

nebo

A+(B + C) = (A + B) + C

Klíčová slova:

Pravidlo komutativní

Platí, že:

A . B = B . A

nebo také:

A + B = B + A

Klíčová slova:

Pravidlo distributivní

Platí, že:

A . B + A . C = A(B + C)

nebo také

(A + B).(A + C) = A + B . C

Klíčová slova:

Pravidlo vyloučení třetího

Platí, že:

nebo

Klíčová slova:

Stránka: 1 2 3 (Další)
VŠE

Nacházíte se zde

Negace logického součtu

Logický součin

AND

Logický součet

AND

Logická negace

Zpožďovací člen - Buffer

Negace logického součinu

Pravidlo asociativní

Pravidlo komutativní

Pravidlo distributivní

Pravidlo vyloučení třetího